數學小神探

相遇機率有多大？

　「哎呀！老張，好久沒看到你，你現在早上都沒來公園運動啊？」公園外路邊，兩位老先生聊了起來。

　「喔，老李，真的好久不見！我還是常來公園運動啊！我也納悶怎麼都沒看到你！」老張說。

　「咦！你都幾點來？」老李問。

　「時間不固定啦！不過最早5:30來，7:00前一定會離開，每次來運動半小時左右，你呢？」老張說。

　「那就怪了！我和你的習慣完全一樣，而且這公園又不大，你來我一定會看見，怎麼都遇不到，真是沒緣哪！」老李笑著說，老張也跟著笑了。

　這一天，數學偵探社到公園裡拍攝櫻花，在公園外湊巧聽見了兩個老先生的對話。一會兒，大家找了間速食店休息吃東西，一邊吃，小哲開口說：「剛剛公園那兩個老先生都在早上5:30到7:00間來公園運動半小時，可是都沒相遇，為什麼會這樣？」

　「拜託！5:30到7:00有90分鐘，運動半小時才30分鐘，只占全部時間的三分之一，沒遇到才正常吧！」小傑一邊吃漢堡，一邊發表高論。

　「是這樣算的呵？」小哲感到疑惑。

　「當然哪！這麼簡單！不然怎麼算？」小傑信心滿滿。

　「小維，按照兩個老先生來的時間和停留的時間，他們相遇的機率有多大呀？」社長怡文不聽小傑亂說，直接問小維。

　「我一下子也不知道怎麼算相遇的機率……」小維似乎也有點困惑，不過立刻接著說：「不過，我們可以先分析一下。」

　「那兩個老先生一個叫老張，一個叫老李，因為兩人都在公園停留半小時，所以如果老張5:30就到，那麼6:00才會離開，也就是說，老李在5:30到6:00間到，兩人都會相遇。」小維邊思考邊說。

　「如果老張5:40到呢？」小傑隨口問。

　「你問這個很好笑！5:40到就6:10離開，只要老李在這段時間來，兩人就會遇到哇！」小哲搶著說。

　「知道這個有什麼用？」小傑疑惑著。

　這時小維似乎想到了什麼，拿出紙筆畫了起來，然後指著（圖一）對大家說：「這是一個正方形，下面橫軸代表老張的時間，左邊縱軸代表老李的時間，我把剛剛說的兩個例子畫上去。以老張來看，紅色線段是他待在公園的時間，老李在這段時間內來，兩人就能相遇。」 

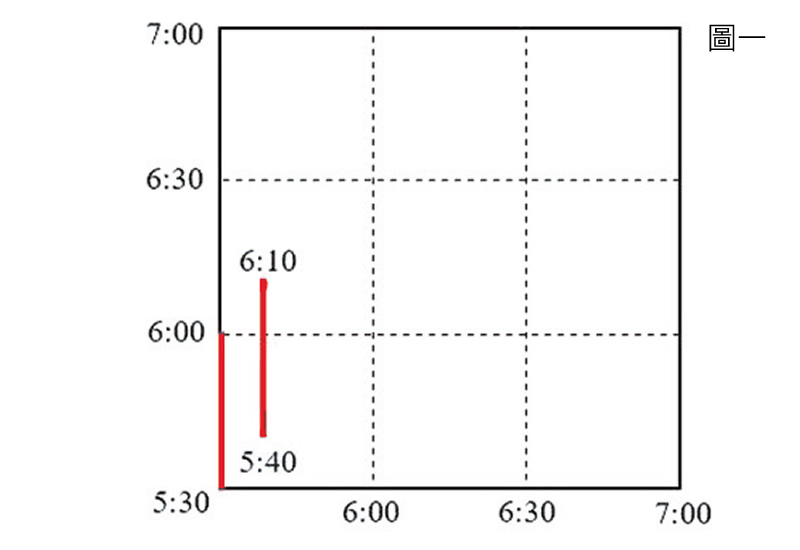
　「可是兩條分開的線段，要怎樣算出相遇的機率呢？」小哲很納悶。

　「啊！不是兩條分開的線段。」怡文似乎靈光乍現，興奮的說：「既然老張5:30之後都有可能到公園，那從5:30開始，這樣的半小時線段應該是連續接在一起的，所以會變成這樣一個區塊（圖二）。」怡文拿起紅筆畫起來。

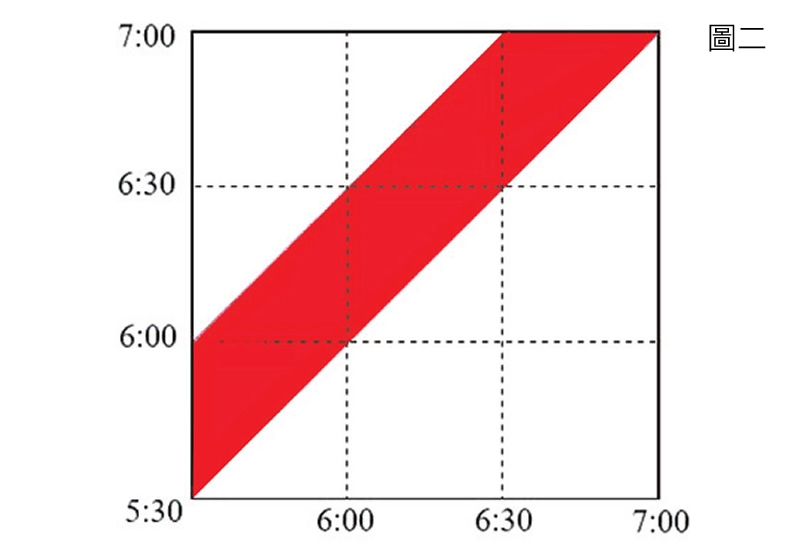
　「哇！是個梯形。」小哲驚訝的說。

　「嗯嗯，沒錯！這樣弄清楚了。以老張到公園的時間來看，這個梯形就是能遇到老李的時間區塊。」小維說。

　「小維，你說『以老張到公園的時間來看』，那如果反過來，以老李到公園的時間來看呢？」怡文發現了問題。

　「如果以老李來看，就能畫出另一個類似的圖（圖三）。」小維又在紙上畫了起來，然後說：「兩張圖合起來的紅色區域，就是兩人能相遇的時間區塊（圖四）。比方說，A點就是老張5:45到、老李6:00到，而B點是老張6:40到、老李6:20到，這兩點都在紅色區域內，表示可遇得到；C點是老張6:15到、老李5:40到，在紅色區域外，表示遇不到。」

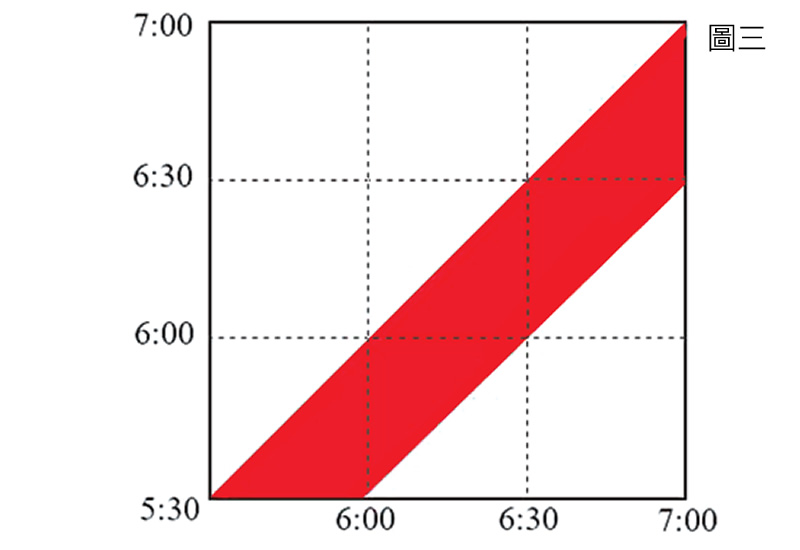
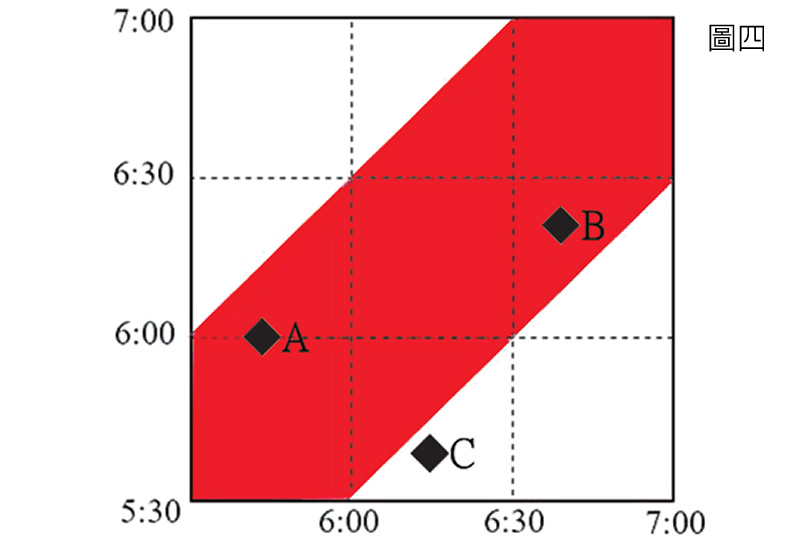
　「還可以變成圖來看，真好玩。」小傑讚嘆說。

　「那要怎樣算相遇的機率呀？」小哲還是不懂。

　「看面積就知道了！」小微笑著說。

　「面積？」小傑和小哲異口同聲的說，不了解小維的意思。

你知道怎樣藉由面積，算出相遇的機率嗎？

解答　

　整個正方形，代表的是兩人所有可能出現在公園的時間；而紅色部分，就是兩人可能相遇的時間。所以，相遇機率就等於紅色區塊與整個正方形的面積比，很容易可以看出是5/9